The Kerr Lab

PYNE-NEDL

(Python-NEURON Network Development Language)

PYNE-NEDL is a framework that combines Python and NEURON to make it easy to build large-scale spiking network simulations. Although NEURON is often considered a detailed single-cell simulator, its efficient event-handling makes it suitable for modeling networks of simple neurons as well.

So far, PYNE-NEDL has been used to create models with up to 100,000 neurons; 10,000 neurons will run in real-time using in-built parallelization methods. PYNE-NEDL also includes modules for plotting and analyzing network activity (including movies, as shown above).

PYNE-NEDL is currently under development, and as a result has limited documentation. However, the source code for a particular PYNE-NEDL model of the sensorimotor system can be downloaded here.

Major contributors to PYNE-NEDL's development include George Chadderdon, Sam Neymotin, and Bill Lytton.

Optima

(HIV Optimization & Analysis Toolbox)

Optima is a cloud-based software package to support prioritization of HIV investment by determining the optimal allocation of resources and coverage levels across programs in specific HIV epidemic settings. Currently, many countries use epidemiological and program reviews to inform HIV strategies to develop budgets. In contrast, Optima uses an integrated analysis of epidemic, program and cost data to determine an optimal distribution of investment to better serve the needs of HIV and health decision-makers and planners.

The unique feature of Optima is its optimization function. For each program area (eg., ART, prevention of mother to child transmission, condom promotion, etc.), the relationships between program cost, coverage, and outcomes are established using country-specific data. A mathematical optimization function is used to calculate the optimal allocation of resources to different program areas to maximize the reduction in new infections, deaths or Disability Adjusted Life Years (DALYs) while minimizing costs. The fully calibrated model combined with these cost-coverage outcome relationships can also generate results on epidemic dynamics, evaluation of past spending, cost-effectiveness of investments, and projected financial commitments.

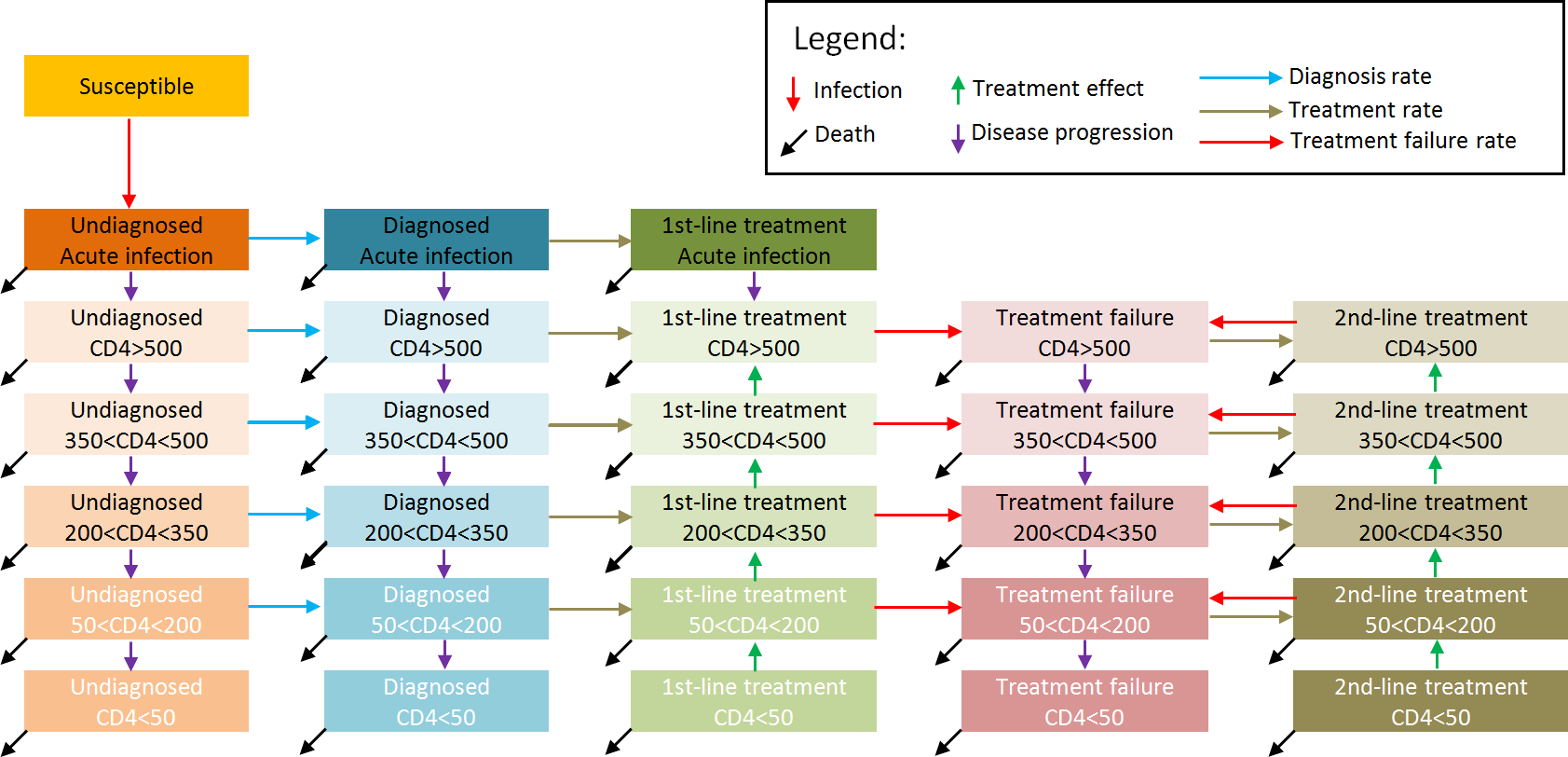
Optima incorporates a mathematical model of HIV transmission and disease progression integrated with a costing and financial analysis framework. Its structure is highly flexible and can accommodate HIV interventions and subpopulations specific to each country. Optima's only fixed aspect is its basic disease progression model, which makes it an HIV model instead of a universal epidemic model.

Optima divides the population into subgroups, based on population type, HIV infection status, HIV diagnosis status, CD4 count, and treatment status (including untreated, first- and second-line treatment, and treatment failure). In contrast to most other HIV models, the population groups are not fixed; an unlimited number of user-defined population groups may be used, including different risk groups (e.g. sex workers, people who inject drugs) and age groups (e.g. children, young adults).

Optima tracks the movement of people between health states. Individuals are assigned to a given population based on their dominant risk; however, parameters can be set to allow multiple transmission risks (e.g. sex workers becoming infected via injecting drug use, drug users occasionally engage in commercial sex). The user enters demographic, epidemiological, behavioral, clinical, and financial data into the model. Data entry is flexible; missing data points do not cause problems, although, the more data points, the more reliable the analysis.

Optima was developed by the Kirby Institute (Cliff Kerr, Robyn Stuart, Andrew Shattock, Richard Gray, Sherrie Kelly, David Wilson), with input from the World Bank (Marelize Gorgens, Nicole Fraser, Markus Haacker, Emiko Masaki).

For further information, please see the Optima website.

ASD

(Adaptive Stochastic Descent)

When standard optimization methods fail to find a satisfactory solution for a parameter fitting problem, a tempting recourse is to adjust parameters manually. While tedious, this approach can be surprisingly powerful.

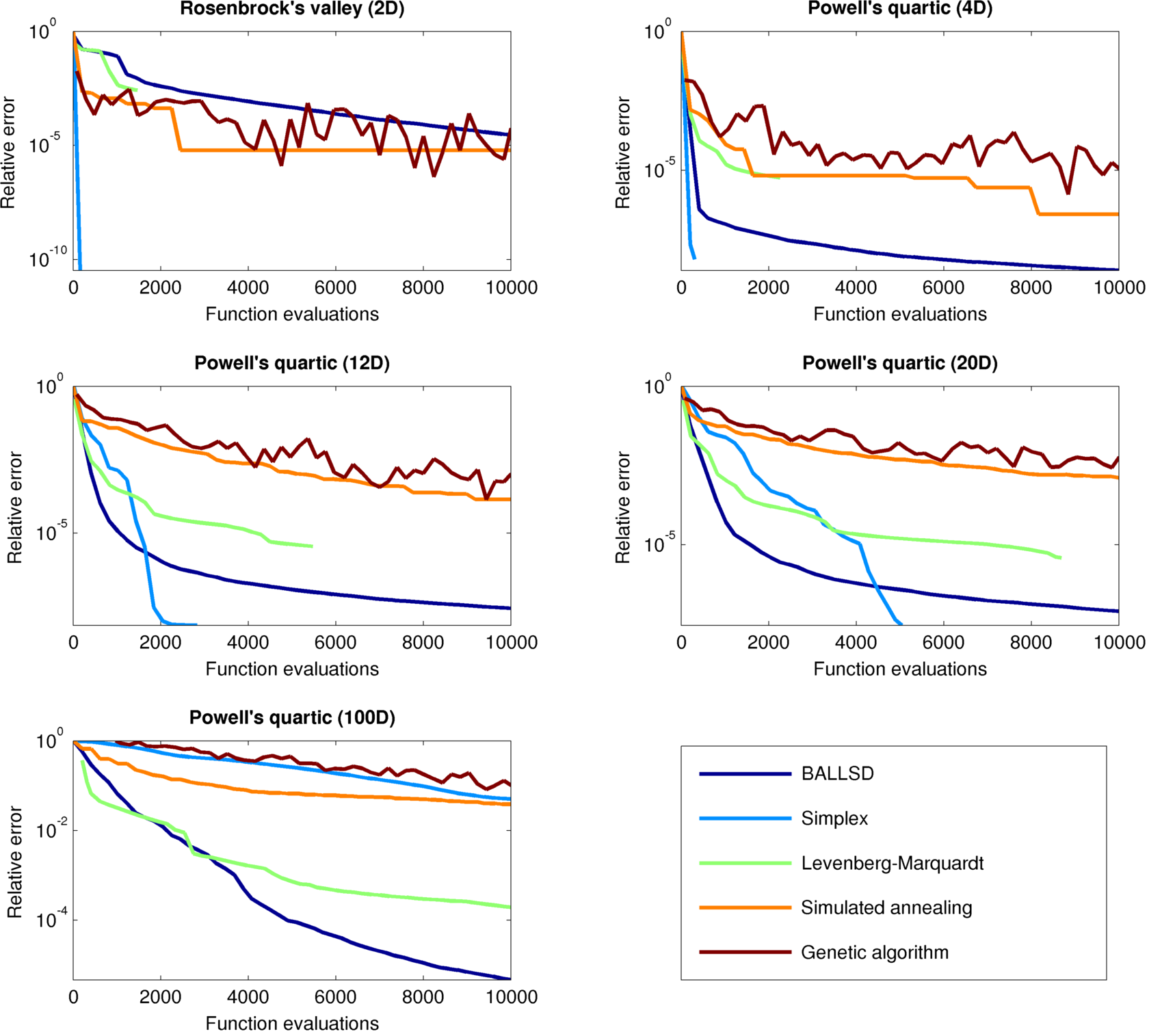
ASD is an optimization algorithm that has been designed to emulate the essential aspects of manual parameter fitting. Specifically, it uses simple Bayesian principles to form probabilistic assumptions about (a) which parameters have the greatest effect on the objective function, and (b) optimal step sizes for each parameter.

For a certain class of optimization problems (namely, those with approximately 5–100 scalar parameter dimensions), ASD is capable of minimizing the objective function with fewer function evaluations than classic optimization methods including simplex, gradient descent, simulated annealing, and genetic algorithms.

ASD for Matlab is available here. ASD for Python is available here. The ASD paper is available here. The supplementary material is available here. The full set of Matlab files used to generate the figures and results in that paper is available here.